A Comprehensive Look at The Multi-Armed Bandit Problem
The multi-armed bandit problem is a class example to demonstrate the exploration versus exploitation dilemma. This post introduces the bandit problem and how to solve it using different exploration strategies.
[toc]
What is Multi-Armed Bandit?
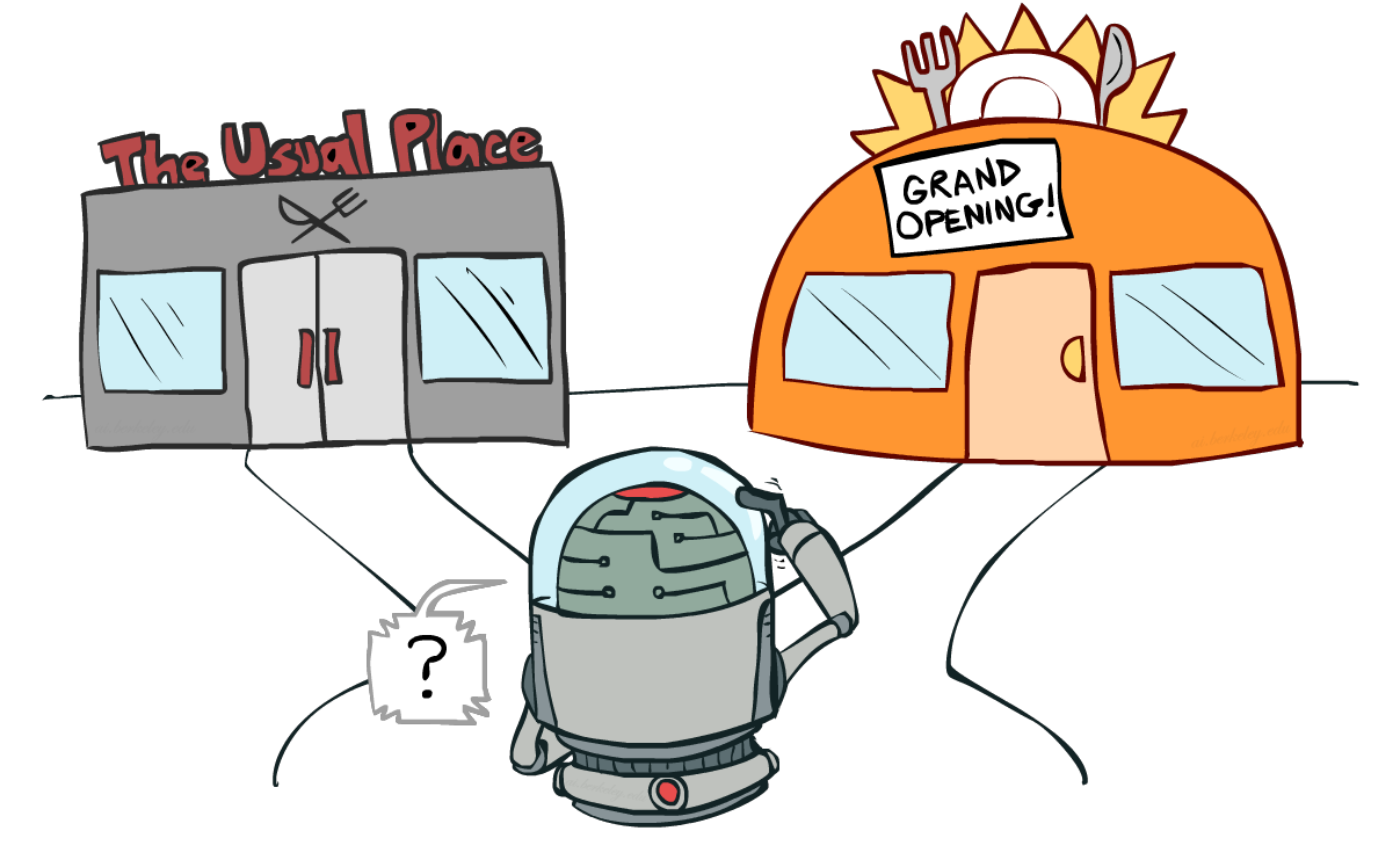
Exploitation vs Exploration
Exploration refers to the discovery of new products, resources, knowledge and opportunities, and it is associated with radical changes and learning through experimentation. Exploitation refers to the refinement of existing products, resources, knowledge and competencies, and is associated with incremental changes and learning through local search (Benner & Tushman, 2003; March, 1991).
The best long-term strategy may involve short-term sacrifices. For example, one exploration trial could be a total failure, but it warns us of not taking that action too often in the future.
Definition
The multi-armed bandit (short: bandit or MAB) can be seen as a set of real distributions $B={R{1},\dots ,R{K}}$, each distribution being associated with the rewards delivered by one of the $K\in \mathbb {N} ^{+}$ levers. Let $\mu {1},\dots ,\mu {K}$ be the mean values associated with these reward distributions.
The gambler iteratively plays one lever per round and observes the associated reward. The objective is to maximize the sum of the collected rewards. The horizon $H$ is the number of rounds that remain to be played.
The loss that we incur due to time/rounds spent due to the learning is called regret. In other words, we want to maximise my reward even during the learning phase. Regret is very aptly named, as it quantifies exactly how much you regret not picking the optimal arm.
The bandit problem is formally equivalent to a one-state Markov decision process.
Bandit Strategies
ε-Greedy Algorithm
According to the ε-greedy algorithm, with a small probability $\epsilon$ we take a random action, but otherwise (which should be the most of the time, probability $1-epsilon$ ) we pick the best action that we have learnt so far.
With probability 1- epsilon – we choose action with maximum value (argmaxa Qt(a))
With probability epsilon – we randomly choose an action from a set of all actions A
Upper Confidence Bounds
Upper Confidence Bound (UCB) is the most widely used solution method for multi-armed bandit problems. This algorithm is based on the principle of optimism in the face of uncertainty.
In other words, the more uncertain we are about an arm, the more important it becomes to explore that arm.
UCB says that we should choose the arm a1 and receive a reward making us less uncertain about its action-value.
For the next trial/timestep, if we still are very uncertain about a1, we will choose it again until the uncertainty is reduced below a threshold.
UCB is actually a family of algorithms. Here, we will discuss UCB1.
UCB1
Steps involved in UCB1:
- Play each of the K actions once, giving initial values for mean rewards corresponding to each action at
- For each round t = K:
- Let Nt(a) represent the number of times action a was played so far
- Play the action at maximising the following expression
- Observe the reward and update the mean reward or expected payoff for the chosen action
Each time a is selected, the uncertainty is presumably reduced: $N_t(a)$ increments, and, as it appears in the denominator, the uncertainty term decreases.
On the other hand, each time an action other than a is selected, t increases, but Nt(a) does not; because t appears in the numerator, the uncertainty estimate increases.
Regret Comparison
Among all the algorithms given in this article, only the UCB algorithm provides a strategy where the regret increases as log(t), while in the other algorithms we get linear regret with different slopes.
Summary
We need exploration because information is valuable.
In terms of the exploration strategies, we can do no exploration at all, focusing on the short-term returns. Or we occasionally explore at random. Or even further, we explore and we are picky about which options to explore — actions with higher uncertainty are favored because they can provide higher information gain.
References
Blog
Paper
A Comprehensive Look at The Multi-Armed Bandit Problem
